Навигация:
Главная → Все категории → Бетонная смесь

Предел прочности бетона различных марок


Предел прочности бетона различных марок

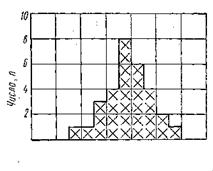
Повсюду, где бы ни применялся бетон, его основным критерием является прочность. Об этом свидетельствует тот факт, что почти каждое бетонное изделие (а из железобетона и предварительно напряженного бетона всегда!) проверяется на прочность. При этом проектант должен в соответствии с маркой бетона задаваться определенной прочностью, так называемой расчетной прочностью при сжатии. Чтобы обеспечить надежность этих значений по ASMW—VW 968, введены контрольные значения прочности для каждого вида бетонной продукции. Однако их выбирают исходя не из средних показателей, а скорее из значения вблизи нижней границы. При построении графика для подбора рецептуры бетона нужно стремиться к определенному среднему значению, которое называют пределом прочности.

Прочность бетона как статистическая характеристика. Если при непрерывном производстве на бетонном заводе или на строительной площадке из каждого замеса брать бетонную смесь и делать из нее кубы для испытания, то можно установить, что каждый куб имеет неодинаковую прочность и что отклонения при каждом испытании от среднего значения довольно велики. Поэтому приближенно из каждого 100-го замеса следует формовать куб для испытания. По результатам испытаний, внесенным в таблицы (так называемые карты), после нескольких операций можно найти наибольшее, наименьшее и среднее значения и очень грубо оценить истинно среднее значение прочности в МПа (табл. 10).

Более наглядно видны разбросы прочности, если их построить в виде диаграмм частотности (рис. 53). При этом методе регистрации с помощью математической модели — гауссовой кривой распределения — могут быть определены в дальнейшем и другие важные характеристики. Кривая распределения и характеризуемые ею зависимости изображены на рис. 54 на основе данных рис. 53. Так как разбросы прочности бетона от одного смесительного узла к другому существенно различаются, на том же рисунке изображены значения прочности бетона, взятого и из другого узла.

Рис. 53. Частотная диаграмма по результатам испытания при сжатии

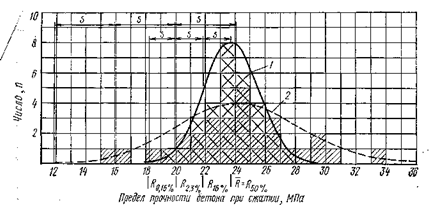
Рис. 54. Частотные диаграммы и математическая модель гауссовой кривой позволяют делать математико-статические прогнозы

Уже упомянутые показатели: – R (иногда Яъо ) как среднее значение, фиксированное проекцией на абсциссу вершины кривой. Яьо % обозначает, что меньшее значение прочности имеют только 50% испытанных образцов. – s (стандартное отклонение) представляет собой расстояние между вершиной и переломной точкой кривой. На основе этих исходных величин можно вывести три других важных критерия: – Ri6% —прочность, получаемая проектированием точки перелома кривой на абсциссу. Следует иметь в виду, что при оценке этой прочности отдельные результаты находятся в области ниже 16%; – 2,3% —значение прочности, соответствующее расстоянию 2s от вершины. Процентное выражение имеет аналогичное значение. – 0,15%—значение прочности,еоот-ветствующее расстоянию 3s от вершины.

В нормах и правилах для бетонных изделий назначается расчетная прочность, например для железобетонных изделий, работающих на изгиб, 60% требуемой марки; для марки В 300 с расчетной прочностью 18 МПа должна, естественно, обеспечиваться очень высокая статистически гарантированная надежность. Поэтому понятно, что ей соответствует очень надежное значение прочности i?o,i5% (в первом приближении). На основе математико-статистических зависимостей, однако, невозможно при контроле качества ориентироваться на такое значение. Поэтому, согласно ASMW—VW 968, контрольная прочность хк должна быть обеспечена с 2,3%-ной вероятностью отказа. Естественно, что существует теоретическая связь между расчетной прочностью и контрольным значением хк.

Рассмотренные до сих пор значения прочности бетона имеют особое значение, так как практически из них выводятся пределы прочности Rz, на которые как на среднее значение ориентируется рецептура бетонной продукции. Использование хк в качестве контрольного значения позволяет практику определить надежность, с которой он выпускает продукцию, и тем самым при хорошей организации и тщательном контроле работать экономичнее.

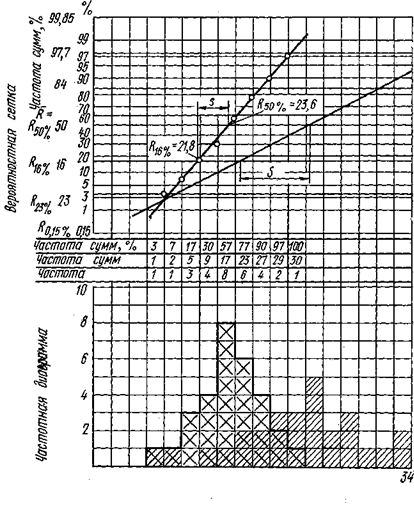
Рис. 55. Графический метод приближения для определения значения стандартного отклонения s из частотной диаграммы (тот же пример, что и на рис. 53 и 54)

Руководитель производства может в зависимости от разброса прочности устанавливать предел прочности Rz. Если у него нет опытных данных, он может выбрать из табл. 11 значения предела прочности, вычисленные по формуле Rz=xK+2 макс с максимальным разбросом прочностей бетона. Если же он располагает действительным разбросом прочности, определенным по результатам испытаний, например, месячной продукции на бетонном заводе, то он может взять за основу эти данные и использовать их в своей дальнейшей работе либо подставить в вышеприведенную формулу вместо Ямакс (не следует никогда работать со значениями s меньше 2,5 н/мм2).

Определить стандартное отклонение прочности на основании результатов испытаний — по существу значит определить качество бетона. Оно под-считывается в разд. 6.4. Здесь же рассмотрим весьма наглядный, но приближенный графический метод с использованием данных, приведенных в табл. 10 и на рис. 53 и 54. Построенная по данным табл. 10 (см. рис. 53) гистограмма увеличена на три графы. В графе «частота» проставляют число испытаний на прочность в интервале; в графе «частота суммы» суммируют предыдущие значения в направлении слева направо и помещают в верхнюю строку истинное значение (т. е. последнее число из предыдущей строки), равное 100%. Обычным расчетом получают все остальные значения для «частоты суммы в ». Значение этой последней строки переносят в «вероятностную сетку» как точку пересечения частоты суммы (ординаты) и прочности (абсциссы), но на правой стороне каждого интервала прочности. Эти точки визуально можно соединить прямой. Точки пересечения полученных прямых со значением ординат 50 и 16 дадут интересующие нас значения прочности R и Ri6%.

Заштрихованная область иллюстрирует оценку результатов, полученных в других опытах, с гораздо большим разбросом прочности, а следовательно, и с большим стандартным отклонением результатов прочностных испытаний.

Из приведенной формулы для определения Rz, как и из рис. 55, можно понять, как велико значение того, чтобы бетонный узел работал с малыми колебаниями прочностных показателей.

Более высокая средняя прочность была обеспечена при меньшем В/Ц, т. е. практически при более высоком содержании цемента.

Разброс результатов испытания образцов цемента на прочность показывает, насколько надежно работает предприятие. Учет разброса значений при определенной контрольной прочности и установление предела прочности Rz экономически стимулируют изготовление бетона более высокого качества, лучшую организацию производства и контроля.



Похожие статьи:
Контроль прочности бетона

Навигация:
Главная → Все категории → Бетонная смесь

Статьи по теме:





Главная → Справочник → Статьи → Блог → Форум