Навигация:
Главная → Все категории → Фундаменты

Представления о перспективных методах расчета оснований фундаментов с учетом нелинейных и реологических свойств


Представления о перспективных методах расчета оснований фундаментов с учетом нелинейных и реологических свойств

На современном этапе развития нелинейного подхода к решению задач расчета грунтовых оснований сформировалось в основном два направления — нелинейно-упругое и упругопластическое.

Нелинейно-упругое направление базируется на нелинейных зависимостях между напряжениями и деформациями (физическая нелинейность) и деформациями и перемещениями (геометрическая нелинейность). В большинстве существующих расчетных методов геометрический характер нелинейности игнорируется, что может быть признано не совсем справедливым при рассмотрении задач со значительными нагрузками и большими значениями перемещений, возможными при наступлении предельного равновесия или при расчетах оснований, сложенных слабыми грунтами.

В нелинейной теории упругости используют уравнения равновесия, а также геометрические и физические соотношения, причем первые два типа уравнений тождественны применяемым в теории упругости, а физические соотношения нередко используют в виде обобщенного закона Гука, но с переменными, зависящими от уровня напряженного состояния: модулем деформации Е и коэффициентом поперечной деформации v. Значения этих характеристик определяют, как правило, на основании феноменологических (опытных) данных.

При решении нелинейных задач методы интегрирования, используемые в классической теории упругости, неприменимы. Поэтому приходится прибегать к методу последовательных приближений, заменяющему интегрирование решением последовательности линейных задач теории упругости, называемым методом упругих решений.

Нелинейно-упругие решения позволяют получать более достоверные результаты по сравнению с линейно-упругими, однако не дают возможности учитывать в расчетах режим изменения внешней нагрузки (траекторию нагружения), реологию деформирования, а также несоосность тензоров напряжений и деформаций. Это, несомненно, накладывает некоторые ограничения на применения нелинейных решений к грунтовым массивам.

Упругопластический подход основывается на раздельном описании упругих и пластических деформаций различными физическими зависимостями. Согласно таким представлениям, использование дифференциальных уравнений, связывающих напряжения с пластическими и полными деформациями, совместно с процедурой пошагового (последовательного) загружения грунтов в соответствии с очередностью изменения и приложения внешних нагрузок позволяет учитывать режим (траекторию) нагружения, а также проявление несоосности тензоров напряжений и деформаций и некоторую другую специфику работы грунтов, что неосуществимо в рамках нелинейной теории упругости. Однако и этот путь решения инженерных задач имеет недостатки. В частности, он не позволяет учитывать нелинейность в упругой области деформирования и реологические процессы, происходящие в грунтах.

Процесс деформирования грунтов во времени рассматривается в настоящее время с позиций теории, называемой теорией консолидации (уплотнения), построенной на основе использования трехфазной модели грунтовой среды, позволяющей учитывать и реологию деформирования скелета грунта. Однако и эта теория не свободна от некоторых недостатков, так как рассматривает в основном водонасыщенные грунты в условиях линейного деформирования, что не всегда соответствует реальным условиям работы грунтов в основаниях сооружений.

Таким образом, в настоящее время сложилось положение, при котором напряженно-деформированное состояние грунтовой среды рассматривается с позиции различных моделей (линейно-упругой, нелинейно-упругой или упругопластичной), а затухание осадки во времени оценивается на основе теории консолидации, предполагающей иные исходные предпосылки при построении исходных уравнений, используемых для решения различных задач. Поэтому имеет смысл построение расчетной модели, которая представляла бы собой синтез нелинейно-упругой и упругопластических теорий и позволяла проследить процесс деформирования грунтов во времени.

В основу модели следует положить следующие исходные предпосылки: справедлива гипотеза о малости деформаций при конечной величине перемещений; внешняя нагрузка изменяется Во времени по некоторому закону, причем характер ее изменения статичен, т. е. силы инерции не учитываются; скелет грунта обладает нелинейными и реологическими свойствами, определяемыми на основании феноменологических (опытных) данных.

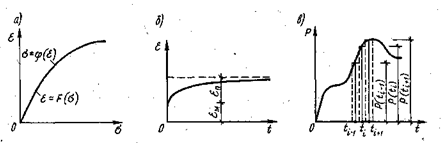
Рис. 2.27. Графики зависимостей: а — деформаций от напряжений; б — деформаций ползучести от времени; в — внешней нагрузки от времени

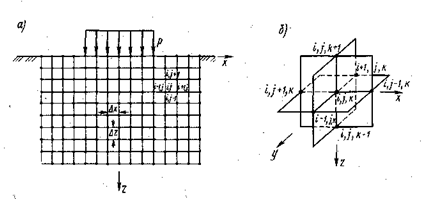
Рис. 2.28. Разбивка основания сеткой метода конечных разностей при плоской (а) и пространственной (б) задачах

нейности деформирования обратит уравнения (2.50) в зависимости Ламе, используемые в теории упругости.
При интегрировании системы уравнений (2.50) возникают неопределимые математические трудности, поэтому для получения инженерных решений в численном виде необходимо воспользоваться методом интегральных оценок, который позволяет линеаризовать задачу в физической области. Сущность метода заключается в фиксации процессов ползучести и изменяющегося режима внешнего нагружения (рис. 2.27, в) в рассматриваемый период времени. Такой подход превращает нелинейные интегродифференциальные уравнения (2.50) в нелинейные дифференциальные для рассматриваемого интервала загружения. Решение в этом случае отыскивается с помощью методов конечных разностей, записанных для плоского или объемного элемента (рис. 2.28), и последовательных приближений, позволяющих заменить нелинейную задачу многократным решением систем нелинейных алгебраических уравнений второго порядка начиная с упругой области деформирования. Результат считается полученным, если разница между двумя последними итерациями не превышает заранее заданной точности расчета в пределах рассматриваемого временного интервала.

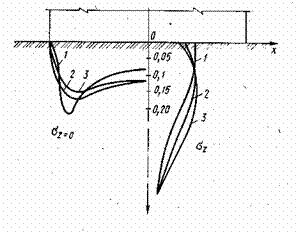
Рис. 2.29. Напряженное состояние в основании жесткого штампа при линейном (1), нелинейном упруго-ползучем (2) основаниях и результаты опытных данных (5)

Проследить весь процесс деформирования грунтового основания можно с помощью просмотра всего временного интервала внешнего загружения (см. рис. 2.27, в). Получение численного решения возможно только с помощью программного обеспечения современных быстродействующих ЭВМ. Для иллюстрации возможностей нелинейного упругоползучего решения приведем результат расчета пылевато-глинистого основания в условиях плоской задачи, которое загружалось в лабораторных условиях жестким штампом (рис. 2.29). Как видно из этогс рисунка, теоретическое решение с учетом реологических свойсп и нелинейности деформирования ближе совпадает с экспериментальными значениями, чем результаты линейного решения.

Применение метода расчета, учитывающего нелинейные и реологические свойства при деформировании грунтовых оснований, позволяет не только более полно учитывать реальные свойства оснований, но и проследить характер изменения напряженно-деформированного состояния в процессе стационарного (неизменяемого) и нестационарного (изменяемого) нагружения, тем самым позволяя изыскать дополнительные резервы несущей способности оснований, что приведет к экономии материальных средств при строительстве и эксплуатации оснований и фундаментов.



Похожие статьи:
Фундаменты глубокого заложения

Навигация:
Главная → Все категории → Фундаменты

Статьи по теме:





Главная → Справочник → Статьи → Блог → Форум